Práctico: Correlación (S06)
6.1 Correlación
Lectura asociada
Contenidos
Diagramas de dispersión (scatter plots): correlación positiva, negativa, nula
Covarianza
Coeficiente de correlación r de Pearson
6.2 Representando la relación entre dos variables: desempeño en literatura y matemáticas
Seguramente alguna vez escuchaste frases como “Lo mío son las letras, soy muy malo para los números”, o al revés, pero ¿qué dicen los datos respecto a esto?
Imagina que se aplican pruebas de desempeño en literatura y matemáticas a adolescentes entre 11 y 15 años que cursan Educación Secundaria en Uruguay.
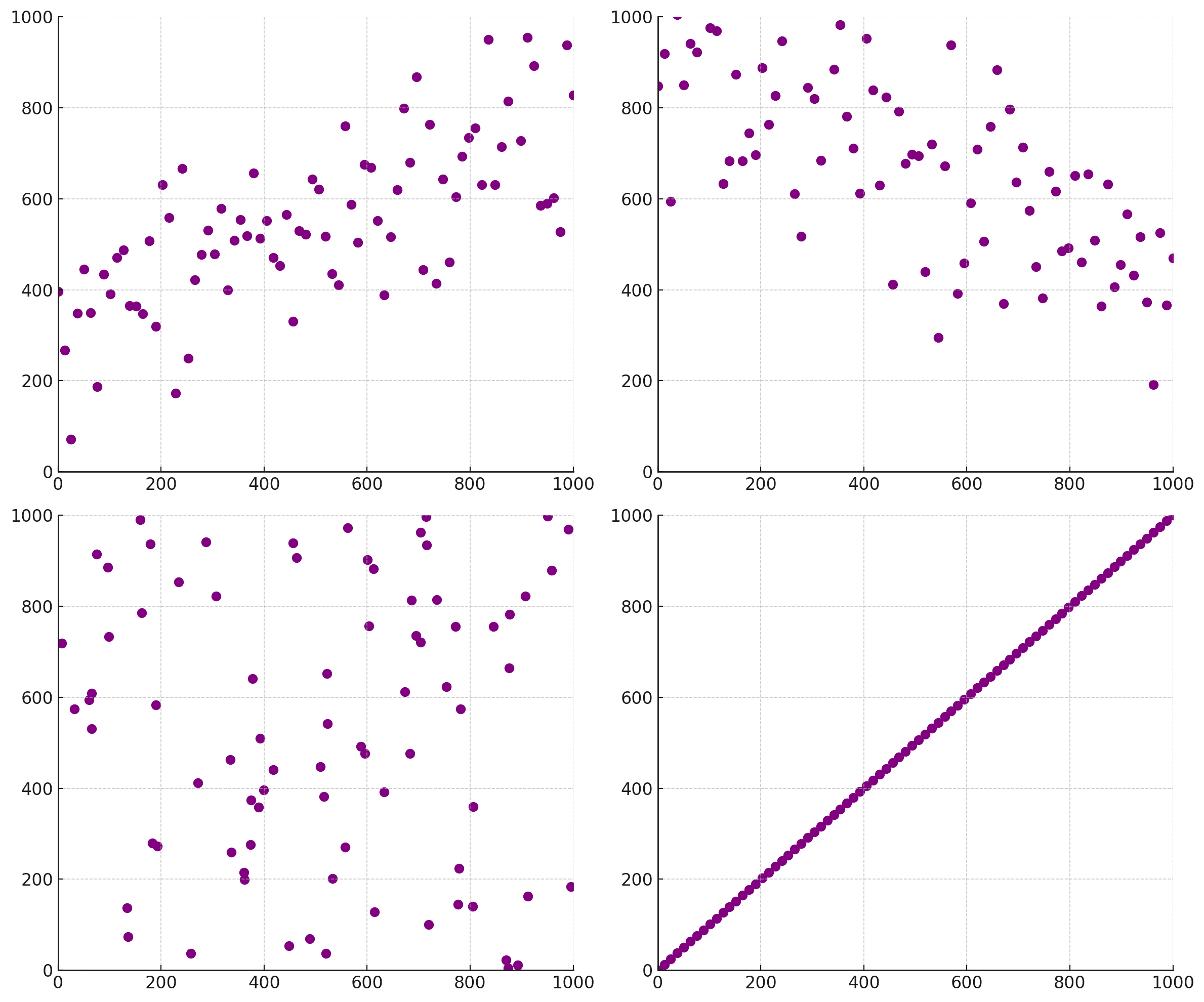
- Observa los siguientes diagramas de dispersión. ¿Qué representa cada punto violeta? ¿Y los ejes x e y?
- En tu opinión ¿Cuál de los diagramas representaría mejor la relación entre los desempeños en literatura y matemáticas?
¿Qué tal si miramos datos reales? Ingresa al panel de análisis y localiza la base correspondiente al Segundo Estudio Regional Comparativo y Explicativo (SERCE).
Activa el botón Acerca de la base para recordar de qué se trata
Selecciona las variables Literatura y Matemáticas y obtiene un diagrama de dispersión
¿Necesitás ayuda?
Aquí te mostramos un ejemplo de la base ENDIS
Gráfico de dispersión > seleccionar variable 1 > seleccionar variable 2
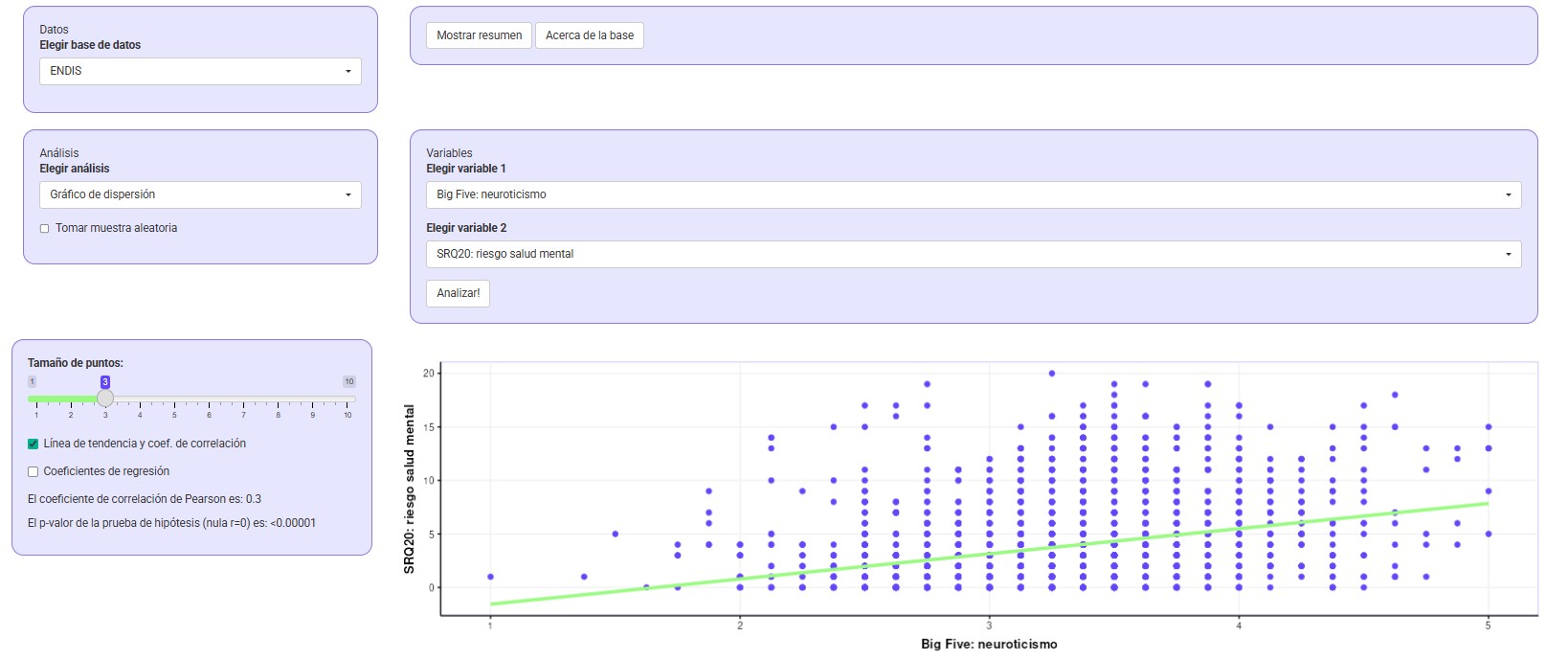
Interpreta el diagrama de dispersión obtenido. Compara estos resultados con tu estimación inicial
Interpreta el valor r de Pearson observado en el panel
Discute si las siguientes afirmaciones son compatibles con el resultado obtenido:
- Los puntajes en matemática y literatura son independientes
- Si un estudiante tiene un desempeño alto en matemática es probable que tenga un desempeño alto en literatura
- Si un estudiante tiene un desempeño alto en literatura es probable que tenga un desempeño bajo en matemática
- Si un estudiante tiene un desempeño alto en literatura es seguro que también tendrá un desempeño alto en matemática, y viceversa
Ahora realiza un gráfico de dispersión para las variables Matemática y Edad. Señala la opción es correcta:
- La edad y el puntaje en matemática muestran una relación negativa
- A mayor edad mejor desempeño en matemática
- El coeficiente de correlación de Pearson es negativo indicando que a menor edad menor desempeño en matemática
- La edad y el puntaje en matemática son dos variables que no covarían
6.3 Covarianza: ¿Qué significa que dos variables “cambien juntas”?
Ingresa al Panel de análisis de datos cuanti.psico.edu.uy/panel
Selecciona la base de datos ARISTAS
Activa el botón Acerca de la base para recordar de qué se trata, con especial atención en las dimensiones del módulo socioemocional de Aristas. Además, puedes encontrar algunos ejemplos de ítems del cuestionario presentado a los estudiantes en este video de la semana 01 de este curso
Plantea tus hipótesis respecto a la relación entre los siguientes pares de variables:
Motivación_y_autorregulación (variable 1) y Habilidades_interpersonales (variable 2)
Motivación_y_autorregulación y Habilidades_intrapersonales
Habilidades_interpersonales y Habilidades_intrapersonales
Antes de activar el panel, dibuja un gráfico de dispersión para cada par de variables en base a tu conocimiento previo o incluso tu intuición al respecto (es decir, 3 diagramas de dispersión). Luego dibuja la línea recta que mejor resume el patrón de los datos.
¿Cuál crees que sería el signo y valor del coeficiente r de Parson en cada caso?
Ahora obtené los mismos gráficos en el panel de análisis. ¿Qué tan distinto es respecto al tuyo? Interpreta la magnitud y dirección de la correlación.
Selecciona otra base de datos ¿Para qué variables dirías que existe una asociación débil? ¿Moderada? ¿Fuerte? ¿Son esas asociaciones positivas o negativas? Formula tus hipótesis y luego realiza el análisis de correlación para las variables de interés.
6.4 Y para terminar, un par de ejercicios múltiple opción
En una investigación sobre rendimiento escolar en Uruguay que empleaba una muestra de 2.372 niños de entre 7 y 10 años, el coeficiente de correlación calculado para las variables ingreso del hogar y puntaje en una prueba de lenguaje fue de r = 0,692. A partir de ese resultado se puede afirmar que:
- La covarianza entre las variables ingreso del hogar y el puntaje de lengua es negativa
- A medida que aumenta el ingreso del hogar, disminuye el rendimiento en lenguaje de los niños de entre 7 y 10 años en el país
- Existe una relación lineal positiva entre el ingreso del hogar y el puntaje en la prueba de lenguaje para los niños de entre 7 y 10 años en Uruguay
- Existe una correlación negativa entre el ingreso del hogar y el desempeño en la prueba de lenguaje en la muestra estudiada
En una investigación reciente sobre competitividad se analizó la relación entre la ansiedad de las personas y el número de errores que estas cometían en un test numérico. Se correlacionaron ambas variables (nivel de ansiedad y número de errores) y se obtuvo un r = 0,734. De estos resultados podemos inferir:
- Dado que el coeficiente de correlación es menor que 1, no existe una correlación entre ambas variables
- Dado que el coeficiente de correlación es positivo, aciertan mayor cantidad de veces cuanto más ansiosas son
- Dado que el coeficiente de correlación es positivo, cometen mayor número de errores cuanto más ansiosas son
- La covarianza entre nivel de ansiedad y número de errores es negativa
Ingresa al panel y selecciona la base de datos Encuesta estudiantes de cuanti. Realiza un gráfico de dispersión para las variables horas de sueño y grado de satisfacción con la vida. La opción correcta es:
- No hay relación entre ambas variables
- Cuantas más horas de sueño, menor es el grado de satisfacción con la vida
- De acuerdo con el coeficiente r de Pearson, la covarianza entre las variables es positiva
- Hay una correlación negativa entre ambas variables