Práctico: Describir los datos - varianza y desvío estándar (S04)
4.1 Varianza y desvío estándar
Lectura asociada
Capítulo 2. Describir los datos Desde 2.8 La varianza en adelante
Contenidos
- Medidas de dispersión: varianza y desvío estándar
4.2 Las variables varían: Tomando nuestros primeros datos
El ejercicio de hoy consiste en adivinar la edad de un conjunto de personas a partir de su foto.
- Ingresa a este formulario 🔗 y adivina las edades de las fotos. Anota en una hoja las iniciales de cada foto y la edad que estimaste.
Conforma grupos de 5 personas
Discute con tus compañeros cómo varían las estimaciones de las fotografías en el grupo
Seleccionen la foto para la que hubo menos variabilidad (es decir, más acuerdo) en las edades y la foto para la que hubo más variabilidad (es decir, mayor desacuerdo) en las edades
Para cada una de las dos fotos seleccionadas:
Realicen una tabla recabando las edades estimadas por cada uno de los integrantes del grupo
¿Cuál es el rango de las estimaciones para la foto?
Calcular la mediana de edad para la foto (pista: ordeno los datos de menor a mayor y encuentro el valor que cae en la posición que divide mi muestra en dos)
Calcular la media (o promedio) de edad para la foto
Calcular la suma de los desvíos cuadráticos de edad para la foto
Calcular la varianza de edad para la foto
Calcular la desviación estándar (o desvío estándar, o desviación típica, o desvío típico) de la edad para la foto
¿Necesitás ayuda?
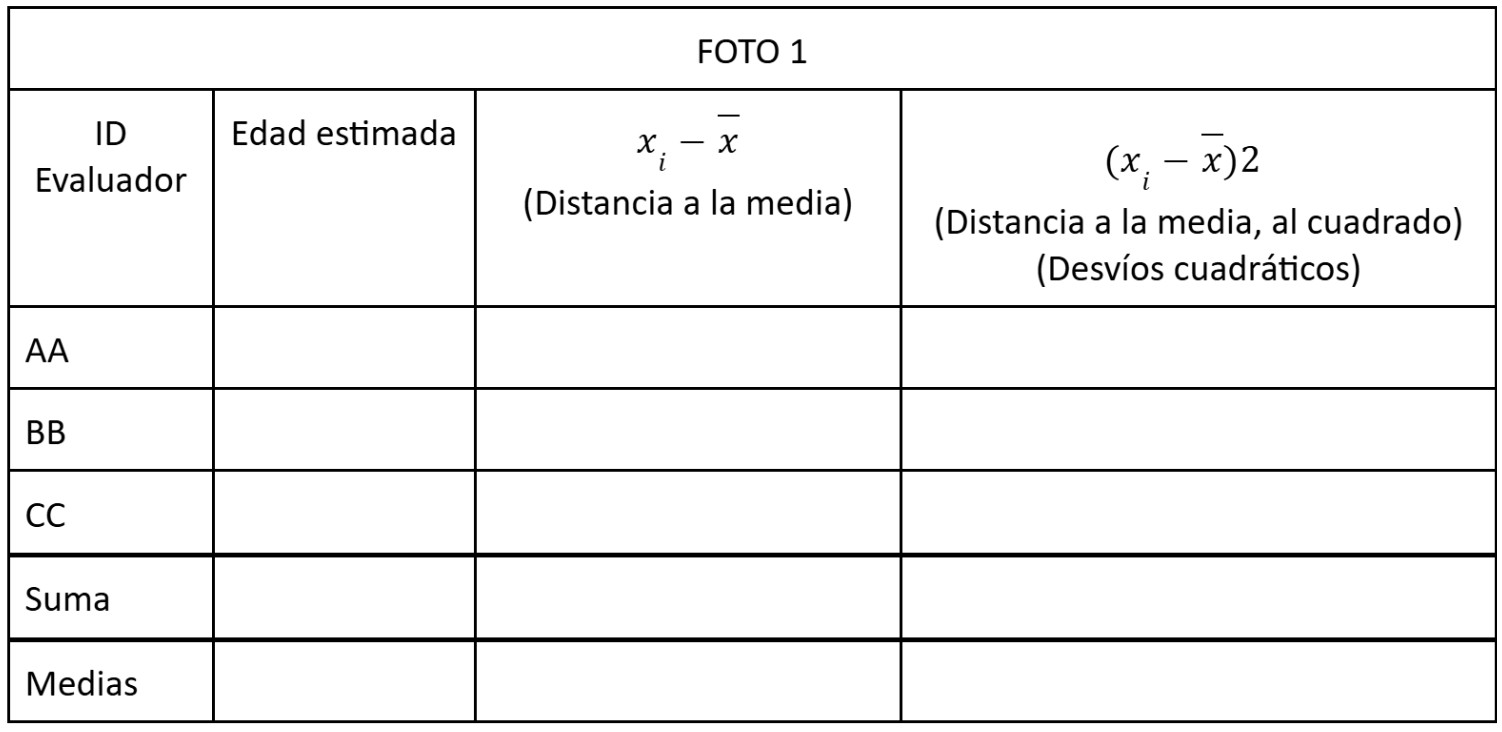
¿Cómo se relaciona la varianza con la edad promedio? ¿Y la desviación estándar con la edad promedio? Discute si uno de los estadísticos resulta más intuitivo
Compara e interpreta las varianzas y las desviaciones estándar para las dos fotos seleccionadas
¿Qué nos dicen estos estadísticos descriptivos de la incertidumbre que tenemos sobre la edad de los fotografiados?
¿Qué habría pasado con la varianza y el desvío estándar si uno de los integrantes del grupo hubiera estimado una edad extrema como 100 años?
Ingresa a esta página 🔗. Observa las estimaciones de todos los compañeros de cuanti
¿Cómo es tu estimación comparada con la de todo el grupo de estudiantes?
¿Cómo es la estimación de tu grupo comparada con la de todos los estudiantes de cuanti?
4.3 Y para terminar, un par de ejercicios múltiple opción, como los del parcial
- ¿Por qué motivo se considera al promedio una medida poco robusta?
Porque presenta siempre valores menores a la mediana
Debido a que es una medida derivada de la moda
Porque es el valor que menos se repite en la distribución
Porque es una medida sensible a los valores extremos de la distribución
- Indique cuál de las siguientes afirmaciones sobre la varianza es correcta:
La varianza es el rango de valores que puede tomar la variable
La varianza es un indicador de tendencia central
La varianza siempre es mayor o igual a cero
Es frecuente que la varianza valga 1